Over this weekend, I was reviewing the theorem that the rationals are countable. Most students of theoretical computer science come across it as warm up before the proof by Cantor that the reals are uncountable. The fact that the reals are uncountable is in turn used to prove the existence of undecidable problems, since there is uncountably many problems but only countably many Turing machines.
Usually, the proof given is that of the rational spiral, seen below, with the comment "can be easily seen to expand for every rational".
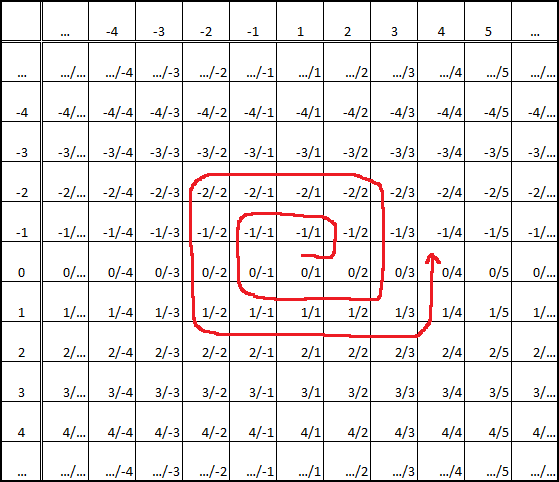 |
| The rational spiral |
That proof was satisfying when I was an undergraduate, but now words such as "can be easily seen", coupled with infinite sets, give rise to doubts. Of course, I am not saying that the rationals are uncountable or that the proof is incorrect, but rather that it is not as insightful as it should be and if the same logic would be applied, one could be lead to mistakes in other, more complicated proofs. So I decided to search online for a proof that would be more rigorous.
This led me to a number of proofs, using specific theorems about infinite sets, constructing bijections and in general, mathematical ideas that might be simple to a mathematician as well as a computer scientist, but are not the bread and butter to the latter. Furthermore, CS students might not be even familiar with them. So I decided that a simpler proof was needed online, and I decided to post it on my blog.
What I noticed was that many proofs identified as a problem that the rationals have countably many representations (for example, the number $0.5$ can be expressed as $\frac{1}{2}$, $\frac{2}{4}$ , $\frac{3}{6}$ and so on) and went in great pain to transform the set of all fractions into a set where each rational has a unique representation. Well, as a computer scientist, I could see that all that clutter was unnecessary, and I proceed to explain myself immediately.
The definition of a countable set is one that has a one-to-one correspondence with the set of natural numbers $\mathbb{N}$. Such a set can then be used to prove other sets countable. Furthermore, any subset of a countable set is of course countable, otherwise the superset would have to be uncountable too.
Does this remind you of anything? Of course, there is a direct analogy with computational complexity here. Instead of sets of binary sequences we have sets of numbers (no change here, I would dare to say), instead of reductions we have one-to-one correspondences (that is, a more specialized type of function between sets) and instead of complexity , our measure is cardinality. A significant difference here is that sets with a finite measure are mostly uninteresting, while sets of $\aleph _{0}$ (countable) and $2^{\aleph _{0}}$ (uncountable) cardinality are the most interesting ones. In the computational complexity setting, sets with a finite measure (on the resources we study) are the most interesting ones, but this difference is from a human perspective than a mathematical one.
With that analogy in mind and since usually we can prove that a problem belongs in a complexity class by a reduction to a problem of that class, we could apply the same principle here and prove that a superset is countable, then work with that. Without further ado, I would like to present the simple proof:
We need a single theorem, that can be easily proven. The proof is omitted for brevity.
The Cartesian product of finitely many countable sets is a countable set.Furthemore, we assume that it is known that the set of integers $\mathbb{Z}$ is countable, which can also easily proven.
Therefore, by the above theorem, it follows that the set of pairs $\mathbb{Q}_{p} = \{ (x,y) | x \in \mathbb{Z} , y \in \mathbb{N} \}$ is countable.
Now we introduce a similar set of all fractions, where the nominator is an integer and the denominator a natural number. That is $ \mathbb{Q}_{f} = \{ \frac{p}{q} | p \in \mathbb{Z} , q \in \mathbb{N} \}$. Note that we treat a fraction as an entity and do not bring the fractions to a canonical form. That is, $\frac{1}{2}$ and $\frac{2}{4}$ are distinguishable elements of $\mathbb{Q}_{f}$. By definition, this set is the set of all possible representations of rationals. Every rational has at least one representation (actually it has countably many as we explained), so if the set of rationals is $\mathbb{Q}$ it follows that $\mathbb{Q} \subset \mathbb{Q}_{f}$ . Therefore, by the principle I explained above, it suffices to show that $\mathbb{Q}_{f}$ is countable. Then, $\mathbb{Q}$ as a subset must be countable too. We do this by a simple one-to-one correspodence between $\mathbb{Q}_{f}$ and $\mathbb{Q}_{p}$.
Namely we have that $f( (x,y) ) = \frac{x}{y}$. The proof that this is a one-to-one correspodence is straightforward, given $x$ and $y$ , we can identify a single fraction and pair with them.
As you can see, this proof is shorter than a small paragraph, two if you include the proof for the Cartesian product, which you don't actually need (you can prove just the case for two sets). I would welcome your suggestions. Does this proof combine the best of the intuitive and the formal world? Does it need improvement? Do you know of similar theorems that could have shorter and more intuitive proofs, without losing their formality?
Am I missing something, or did you just replace a method based on constructing a set S of fractions followed by taking a subset of S to get countability with a method based on constructing a set S of fractions followed by taking a subset of S to argue countability?
ReplyDeleteI don't really see what this accomplishes. In both cases, you're hand-waving away the argument that there is no infinite cardinality smaller than aleph-naught.
Hello and thanks for your comment! When I was writing this the proofs I could find online either proofs that simply gave the rational spiral (thus informal) or proofs that either handwaved the uniqueness of the canonical form or went into quite some trouble to prove it.
ReplyDeleteThe point I want to make is that you can form a bijection with a subset of a countable set and still have a valid proof. This is similar to reducing a problem to another problem, where the instances you get from the reduction have a specific structure and do not cover all possible instances of the problem you reduce to.
Perhaps the above is a trivial example, but the same proof idea could be used extensively.
I find very interesting what you mention about an infinite cardinality smaller than aleph-naught. I would assume this is the smallest one by definition. Any pointers to such a proof or a discussion of this issue would be very interesting!